Keerukus

Algoritmi keerukus on põhioperatsiooni(de) arvu sõltuvusfunktsioon K(n) sisendi(te) suurusest n. Tavaliselt põhioperatsiooni ei defineerita üheselt, mis tähendab, et põhioperatsiooniks võivad olla näiteks:

aritmeetika tehe, võrdlus, omistus
vahel valitakse üks põhioperatsioon ja loetaks selle arvu, näiteks tsüklitingimuse võrdlus
mõnikord kasutatakse ka ridade arvu

Samuti erinevat moodi võib olla defineeritud sisendi suurus. See võib olla:

Sisendandmetemaht(massiivi, faili, andmebaasisuurus)
Sisendparameetriväärtus
Sisendparameetrisuurus(bittide/baitide arv)

Kui hakata mõõtma algoritmi keerukust, siis üheks variandiks oleks kirjutada programm, seejärel lasta tal töötada erineva suurusega ja sisuga andmetega ning mõõta programmi täitmiseks kuluvat aega. Samas ei ole selline metoodika mõistlik. Algoritmi tööaega on keeruline üheselt määrata näiteks sekundites või minutites, sest arvutite võimsused on väga erinevad. Mida rohkem on andmeid, seda paremini hakkab arvutite vaheline võimsus esile kerkima.

Seetõttu on palju mõistlikum kasutada üldist metoodikat, mis erinevalt eksperimentaalsest lähenemisest:

kasutab algoritmi kõrgema taseme esitust, mitte selle realisatsiooni programmina
arvestab kõikvõimalikke sisendandmeid
võimaldab hinnata algoritmi efektiivsust sõltumatult tark-ja riistvaraplatvormist

Lisaks ajalisele keerukusele on võimalik hinnata algoritmi headust mälukasutuse osas ehk kui kiiresti kasvab mälukasutus algandmete suhtes. Võib juhtuda, et algoritm mis kasutab rohkem mälu on ajaliselt vähem keerukas (kiirem) kui algoritm mis on mälukasutuselt efektiivsem, aga ajaliselt keerukam (aeglasem).

Kõige enam kasutatakse keerukuse väljendamiseks asümptootilist keerukust, mille eesmärk on jätta sarnaselt ümardamisele ebaolulised detailid mainimata. Näiteks 1,000,001≈1,000,000

Asümptootiline keerukus ja suure O notatsioon

Algoritm võib töötada erinevatel sisendandmetel väga erineva kiirusega ning kuna tihtipeale meid huvitab kriitiliste süsteemide loomisel see, mis on maksimaalne algoritmi töötamise aeg suvaliste sisendandmete juures, siis räägitakse asümptootilise keerukuse juures tavaliselt halvima juhu keerukusest.

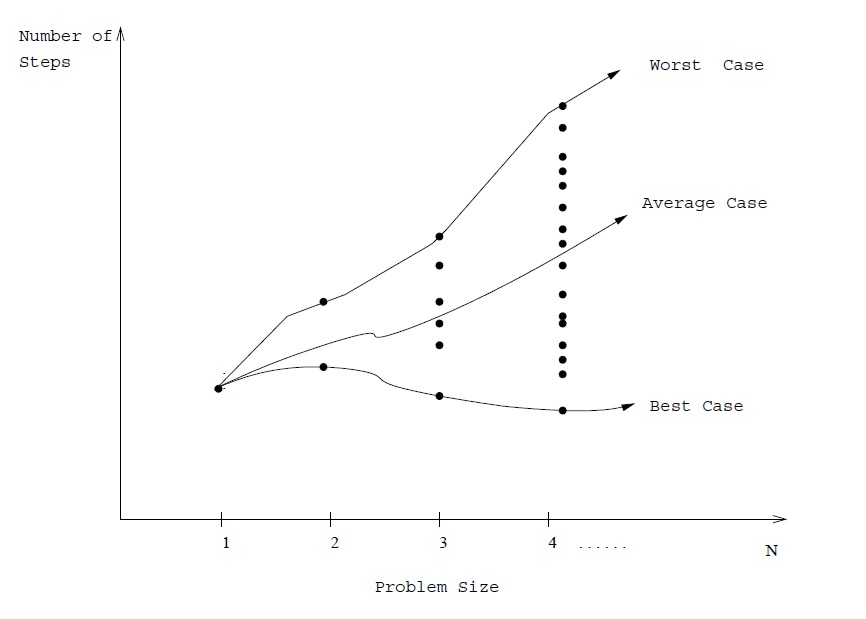
Järgmiseks tähtsaks mõisteks on Suur-O notatsioon, mis on relatiivne algoritmi keerukuse näitaja, mida on mugav väljendada graafiku abil, kus on erinevate keerukusklasside põhioperatsioonide arv sõltuvusest sisendi suurusest.

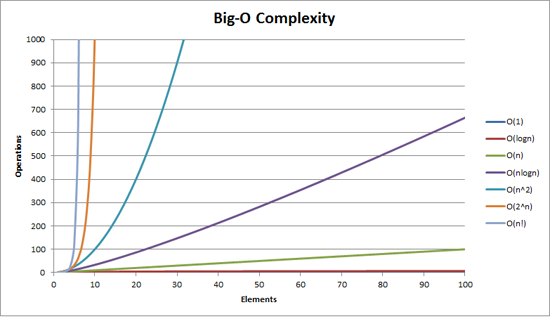
O-notatsiooni abil saab väljendada nii ajalist kui mälulist keerukust. Näiteks algoritmi keerukus on O(n) aja suhtes või algoritm kasutab O(n) ruumi (mälu) algandmete suhtes.

Kui vaadata eraldi keerukusklasse, siis:

O(1)keerukus ei sõltu n-ist

 1 item: 1 second
 10 items: 1 second
 100 items: 1 second

 Tavaliselt O(1) on lihtne käskude järgnevus või mitterekursiivse funktsiooni väljakutse.

 O(n) on lineaarne keerukus

 1 item: 1 second
 10 items: 10 seconds
 100 items: 100 seconds

 O(n) tähendab seega, et sisendi suurenemisel suureneb täitmiseks kuluv aeg võrdeliselt.
 Näiteks ühekordse tsükli korral.
 for(i=0 ;i<n; i++){s;}

 O(n^2) on ruutkeerukus

 1 item: 1 second
 10 items: 100 seconds
 100 items: 1000 seconds

 Näiteks kahekordse tsükli korral peab täitma sisemist tsüklit O(n) korda ja välimist samuti O(n) korda.
 for(j=0; j<n; j++){
  for(k=0; k<n; k++){s;}}

 O(log n) on logaritmiline keerukus

 1 item: 1 second
 10 items: 2 seconds
 100 items: 3 seconds
 1000 items: 4 seconds

 Näiteks kahekordse tsükli korral, kus tsükli indeks varieerub eksponentsiaalselt.
 for(int i=n; i>1; i = i/2){s;}

O notatsiooni omadusi:

Konstantseid kordajaid võib ignoreerida ∀ k > 0, k∙f on O(f)
Kõrgemad astmed kasvavad kiiremini n^r on O(n^s),kui 0 ≤ r ≤ s
Kiiremini kasvav liidetav määrab summa kiiruse näiteks an^4 + bn^3 on O(n^4)
Exponentfunktsioonid kasvavad kiiremini kui astmed näiteks n^20 on O(1.05^n)
Kõik logaritmid kasvavad sama kiirusega

Analüüsime ühte koodijuppi ja määrame selle keerukuse

int find_c(int n)
  int i,j,c
  for(i=1; i < n; i=i*3)
    for(j=0; j < 3*n; j++)
      c++
  for(i=c; i > 0; i--)
    if(odd(random(0...999)))
      for(j=0; j < 3*n; j++)
        c++
    else
      for(j=n; j < n*n; j++)
        c++
  return c

  Vaatame eraldi kahte välimist tsüklit ja määrame nende keerukuse for(i=1; i < n; i=i*3) ja for(i=c; i > 0; i--)
  1)  for(i=1; i < n; i=i*3)
        for(j=0; j < 3*n; j++)
          c++
     Kui alustada seestpoolt, ehk for(j=0; j < 3*n; j++), siis näeme, et j = 0 ja läheb kuni 3*n.
     Sammuks on j++, seega peab iga elemendi kuni 3n läbi käima.
     Seega on selle jupi keerukus O(3n) = O(n), kuna meid huvitab ainult oluline osa,
     kordaja ei oma tähtsust üldise pildi saamiseks.
     Kuna tegemist on tsükliga tsükli sees, siis me peame leidma välimise tsükli keerukuse
     ja korrutama selle sisemise tsükli keerukusega läbi.

     for(i=1; i < n; i=i*3) keerukus on O(log n), kuna me ei käi läbi igat elementi kuni n,
     vaid indeks sammuks on i*3.

     Kui me korrutame läbi sisemise ja välimise tsükli, siis saame üldiseks ploki keerukuseks O(n*log n)

  2) for(i=c; i > 0; i--)
       if(odd(random(0...999)))
         for(j=0; j < 3*n; j++)
           c++
       else
         for(j=n; j < n*n; j++)
           c++

     Välimise tsükli sees on kaks sisemist tsüklit, mille käivitamine sõltub tingimusest, et
     juhuslik arv tuleb paaritu. Kuna tegemist on juhusliku valikuga ning me orienteerume
     halvima juhu keerukusest, siis valime selle sisemise for-tsükli, millel on suurem keerukus.
     Antud juhul on aga mõlema tsükli keerukus O(n), kuigi teine justkui peaks käima läbi n^2 korda,
     siis paneme tähele, et else tsüklis on j=n, ehk me alustame juba n-ist.

     Välimise tsükli for(i=c; i > 0; i--) keerukus on samuti O(n), kuna miski ei viita kordsele
     itereerimisele või suuremale sammule, kui 1.

     Kokku on seega selle ploki keerukus O(n)*O(n) = O(n^2)


  3) Nüüd on alles jäänud ainult mõlema ploki keerukus kokku panna, et saada teada meetodi keerukus.
     Kuna tsüklid on sõltuvad üksteisest
     (teine koodiplokk algab i=c, mida arvutatakse alles esimeses tsükliplokis),
     siis keerukused korrutuvad. O(n*log n) * O(n^2) = O(n^3*log n)

Algoritm on polünomiaalne kui ta on O(n^d) mingi täisarvu d korral. Polünomiaalseid algoritme peetakse efektiivseteks, ehk nad lahendavad ülesande mõistliku ajaga.

Intuitiivne O notatsiooni selgitus: https://stackoverflow.com/questions/487258/what-is-a-plain-english-explanation-of-big-o-notation